Explainer Series: artificial neural networks
An attempt to explain neural networks with a series of digestible diagrams
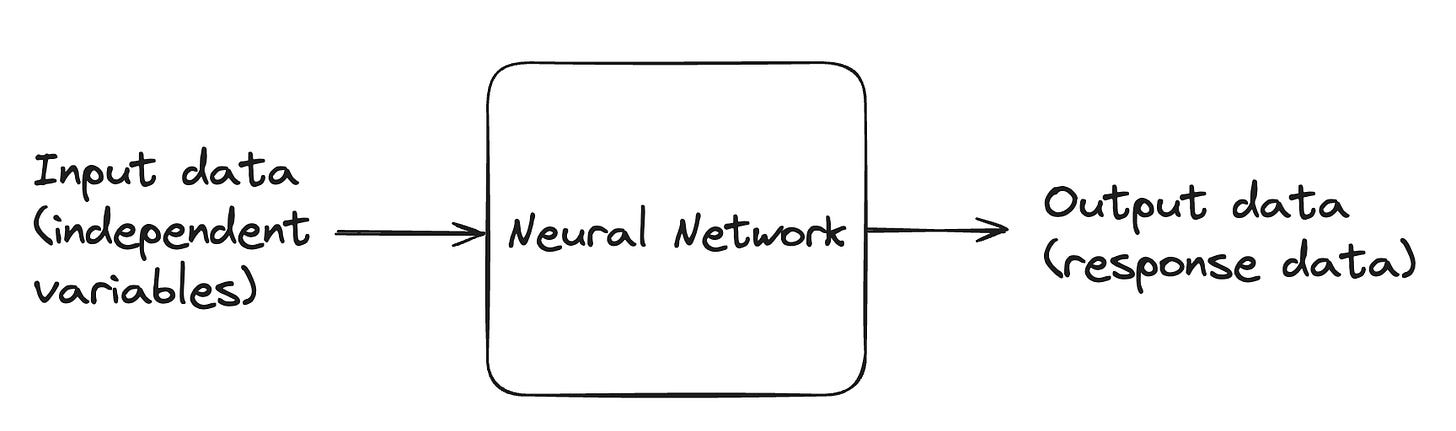
An artificial neural network is a machine learning model designed to act like a biological brain. The model uses nodes (inspired by neurons) connected by edges (inspired by synapses) that are organized into layers.
The input layer comprises of inputs nodes, which are your input or predictor variables. These input nodes have weights or coefficients.
The output layer contains output nodes, which give you the output of your model (i.e. the prediction or response variable).
Between the input and the output layers, exists one or more hidden layers. The nodes in the hidden layer automatically learn patterns in your data — but unlike the input nodes, you don’t specify what they represent. The weights connecting the hidden layers will be determined by training the model on your data (or in other words finding a collection of weights that best map the input data to the output data). The purpose of the hidden layers are to find patterns in the data. The author of the neural network decides how many hidden layers and nodes to include.
If you go to wikipedia to learn about artificial neural networks, you’ll see a diagram like this with references to the neurons and synapses in our brains.
We will build up to explaining this diagram through a series of simpler diagrams. To follow along, I recommend having a pen and paper to sketch these diagrams yourself, along with questions and observations. I will intentionally withhold some details until later in the post, and some topics will remain unexplained, so we can focus on the core functionality the model. If this is your first time digging into the structure of neural nets, it might take a couple read-throughs to understand how everything fits together.
At its core, a neural network maps input values to output values:
What are these inputs and outputs?
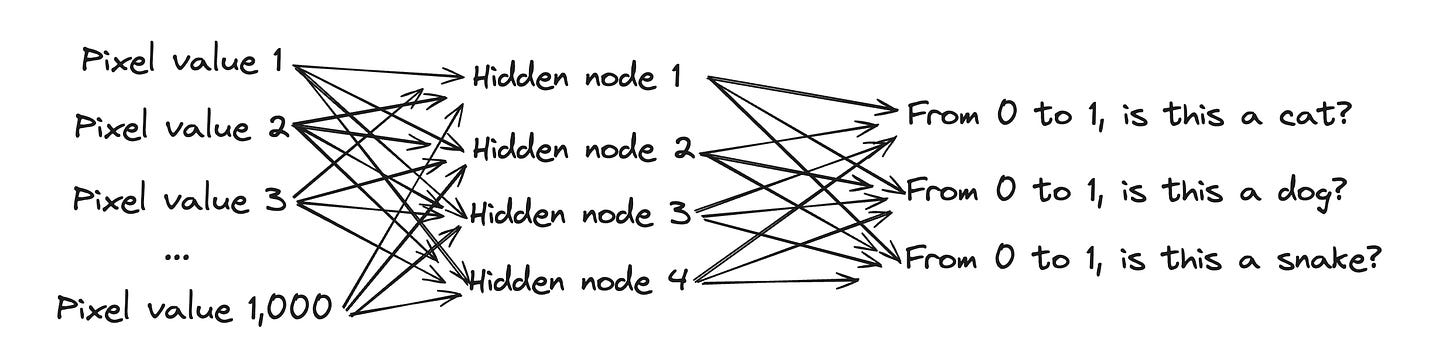
Let’s say we want to classify a greyscale image to determine if it’s a cat, dog, snake, or something else. Our inputs will be pixel values1 ranging from 0 (black) to 255 (white). The outputs will be 3 values ranging from 0 to 1 representing the probability2 that the image is a cat, dog, or snake. If the probability for the ‘Is Cat?’ response variable exceeds a threshold that we set (e.g. .85) , we say that our image is a cat.
The data used to train the neural network will be labeled by a reliable source (e.g. a human manually labeling it) — this is called the truth set. In our training data response variables, we will only have values of 0 or 1, indicating whether a human identified a cat/dog/snake..
When running our classifier model on unlabeled images, it will output probabilities for cat/dog/snake and choose the one closest to 1. If all values are close to 0, we can say our image resembles something else.
What if a Neural Network was just a set of linear regressions?
Let’s pretend that a neural network was just a simple linear regression. If this we’re the case, we would have 3 linear regression equations. The pixel values would be the independent variables for each equation. The cat variable would be the response variable for the first equation — the dog and snake variables would be the response for the second and third equation.
Each pixel would have a corresponding weight — just as each independent variable in a linear regression has its own weight.
Neural networks are similar to a set of linear regressions, but… to get the full picture, we need to talk about the hidden layer(s).
Instead of using the term linear regression, we will now talk about something more general: linear combinations. To calculate a linear combination, we will multiply each pixel value by a weight and add up each weighted pixel value.
Hidden layers
A neural network does not map our inputs directly to our outputs. Instead, there is an intermediary output, called the hidden layer.
The diagram below shows a hidden layer with 4 nodes:
This diagram represents 4 equations. Each equation is a linear combination of the weighted pixel values. However, what makes the hidden layer special is that we’re going to take the result of that linear combination and pass it into an activation function.
Activation function
An activation function is kind of like a light switch that’s either on or off. The outputs are typically close to 0 or close to 1.
So now we can picture our hidden layer like this:
To recap, with the hidden layer, we are calculating a linear combination of our inputs with corresponding weights — then we’re passing the result of the linear combination through the activation function — this gives us the values for the nodes in the hidden layer.
From hidden layer to output
In order to get from our hidden layer to our output layer, we do the same exact step as before. Except instead of going from input data to hidden layer, we now treat our hidden layer as the input.
This diagram represents 3 linear combination equations. We will take each hidden node’s value, multiplied by its weight, and add them all up.
Because our final outputs range from 0 to 1, we will once again pass the results of the linear combinations through the activation function.
Okay I get the structure of the neural network but how do we determine the weights?
Finding the weights of our neural network is called training our model. This is the computationally expensive step that involves lots of data and an algorithm called backpropagation.
Let’s zoom in a little on the weights:
We have established that a neural network is a series of linear combination equations that get passed into activations functions, which in turn get passed as inputs into more linear combination equations, which are then passed into another activation function.
Remember that one record in our data contains 1,000 pixels (our inputs) and the indicators for cat, dog, and snake.
Let’s imagine we need to find out the best weight by brute force — or in other words, lots of trial and error.
We could go to our first record and choose random weights for all of our inputs and hidden nodes.
We run all the various linear combinations: in our case 4 equations (with 1,000 inputs each) for each hidden node, then 3 equations (with 3 inputs each) for each final output.
We check to see how we did — we compare the true output in our data to what outputs we got using our random weights. So if our Is Cat? variable is supposed to be 1, but our results were .42, we would be off by .58.
If we had a super powerful computer, we could hypothetically keep choosing random weights for each record and hidden node until our final outputs looked as close as possible to the true outputs. We could then average these weights across all our records to find the best fit.
This process of finding the right weights is an optimization problem — we want to find out what set of weights result in the best fit between our predicted output values and the actual output values.
In reality, the brute force technique is too inefficient, so we use a technique called backpropagation. Backpropagation is not guaranteed to find the perfect fit for our data, but it balances the tradeoff of computational efficiency and best-fit.
There you have it — a neural network is a set of linear combinations passed through activation functions that are then passed into another set of linear combinations that are then passed through more activation functions. And finding the weights can be achieved through backpropagation - an algorithm that efficiently finds weights that give us the best fit between our predictions and the truth.
So what did I leave out?
In short, a lot. But I hope this provides a nice primer for understanding how neural networks work behind the hood.
In the real world, there are many different types of neural networks with more complex architectures.
Zooming out, it’s important to keep in mind that models are only a piece of the puzzle. When it comes to applying machine learning to real world problems, the problem statement and input data are foundational.
Thanks for reading and leave me a comment if I got something wrong, and I’ll make corrections!
In reality, every pixel probably won’t be an input. We might break down our image into subsections of pixels and take the average of each subsection for our inputs.
Not truly a probability but we can think of it like one.