ML and questions of why (causation)
The core goal of supervised machine learning is curve fitting: how do my inputs map to my outputs. Once some approximation of this mapping is learned, we can feed the model a new input to see if it adequately maps it to the desired output. This mapping of inputs to outputs is underpinned by our inputs having some association with our outputs.
No matter how good this mapping gets, it’s important to recall the saying, “correlation (or more broadly association) does not imply causation.”
So how do we establish causation?
The tried-and-true way is through (randomized, controlled) experiments. The better the experimental design, the stronger we can make the case: X causes Y or, in other words, “if we hadn’t administered some intervention X, then we wouldn’t see some change in Y.” The counterfactual statement is a causal statement.
Can we establish causality without running an experiment?
Yes, but… by making assumptions. If the assumption don’t hold up, neither do the casual claims.
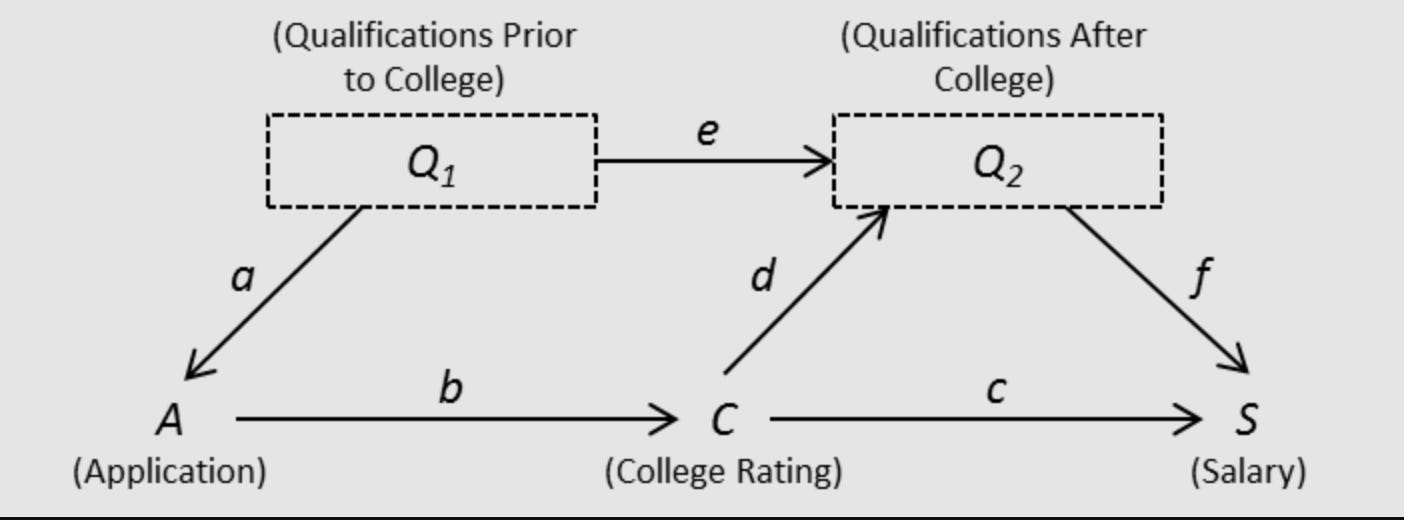
The Book of Why explores Causal diagrams or DAG’s.
These diagrams encode assumptions on causal pathways. Causal models also include nuance by indicating the different causal roles that certain variables can play (e.g. confounders, colliders, suppressors, etc.)
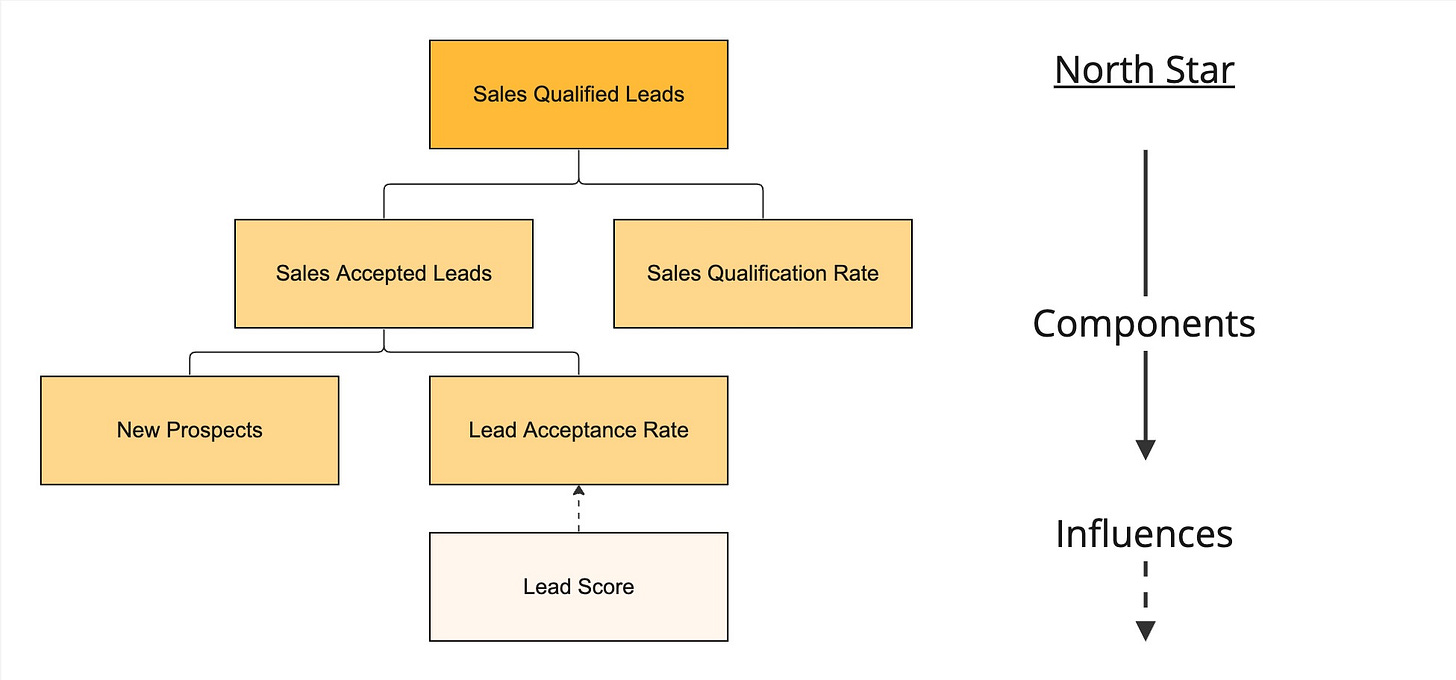
In the less academic business analytics world, there is an idea that’s recently been getting attention called metric trees.
Instead of a DAG with lots of arrows, it’s a simpler tree. At the top of the tree is the north star metric (e.g. sales), under that will be things that leads to sales (e.g. number of opportunities and win rate). or influence it. Under number of opportunities might be number of leads, under that might be website traffic, and so on. This tree is essentially a simplified causal model based on business processes.
Since the tree is hierarchical, it’s interpretation is “leads drive opportunities drives sales” — it doesn’t do a great job at capturing variables with different causal roles (e.g. mediators, confounders), nor does it capture things like feedback loops very well.
Like the causal graph, the metric tree bakes in assumptions about the causal flow. This means if an assumption is wrong or the model is incomplete, the claims won’t hold up.
Where does ML fit into all this?
While a supercharged XGBoost model or a deep neural network might be amazing at mapping inputs to outputs, these approaches aren’t designed to establish causality.
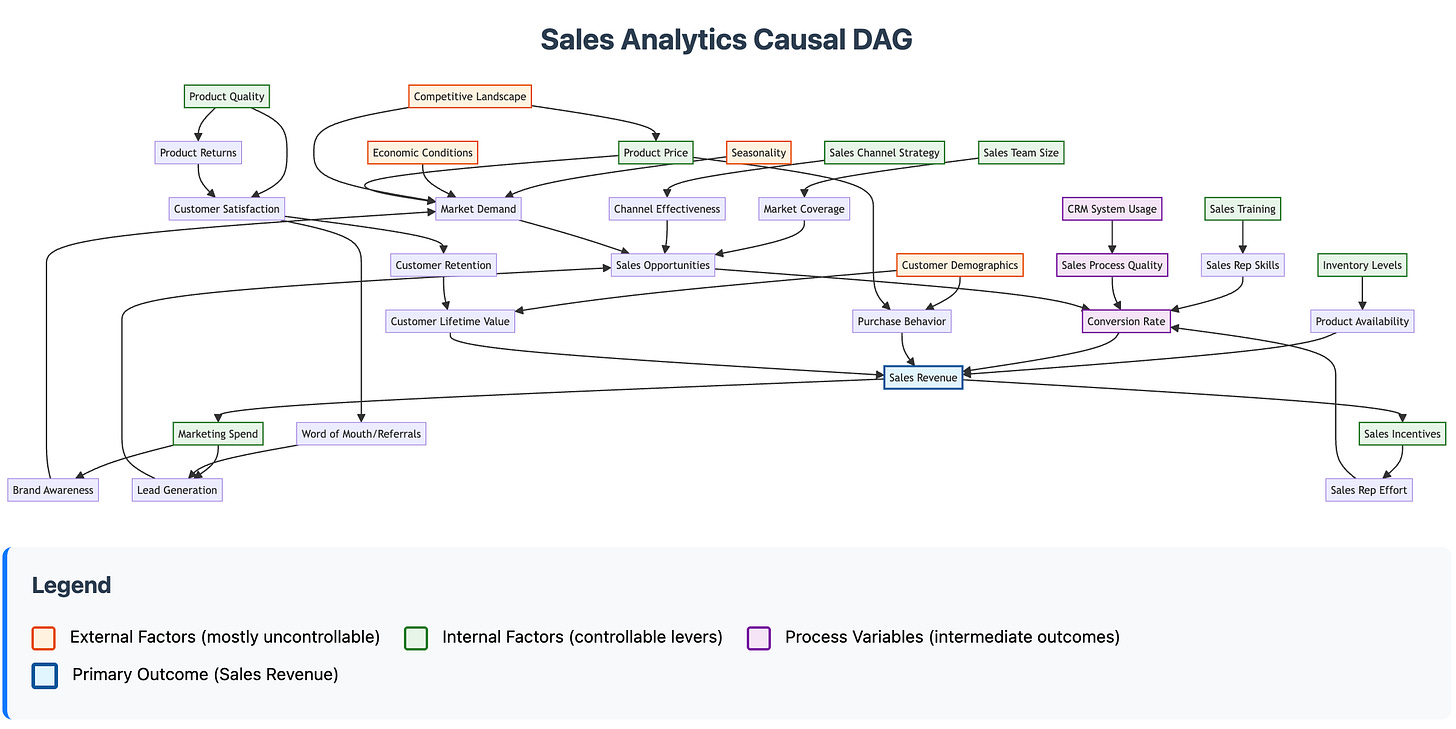
Just as LLM’s are being used to write code in programming applications, I think they can also be helpful for rapid prototyping a causal DAG or a metric tree.
Here’s an example of a Causal DAG in a business context that Claude mocked up:
In other words, not relying on the LLM as a magic 8-ball for your questions, but using the LLM to more efficiently build reliable tools that can help make causal claims.